Tuhaf Boşluklarda Gizlenen Fibonacci Sayıları

ON DÖRT YIL ÖNCE, matematikçiler Dusa McDuff ve Felix Schlenk, yeni yeni çiçek açmaya başlayan gizli bir geometrik bahçeye rastladılar. Çift, çok özel şekillerde sıkıştırılabilen ve katlanabilen ve bir topun içine doldurulabilen belirli bir tür dikdörtgen şekille ilgileniyordu. Merak ettiler: Belirli bir şekil için topun ne kadar büyük olması gerekiyor?

Sonuçları kristalleşmeye başladığında, ortaya çıkan çarpıcı kalıpları ilk başta fark etmediler. Ancak çalışmalarını gözden geçiren bir meslektaş, girişleri doğada ve yüzyıllar boyunca matematikte tekrar tekrar ortaya çıkan bir liste olan ünlü Fibonacci sayılarını fark etti. Örneğin, eski Yunanlılardan beri sanatta, mimaride ve doğada incelenen yüce altın oranla yakından ilişkilidirler.

Cornell Üniversitesi'nden matematikçi Tara Holm, Fibonacci sayıları "matematikçileri her zaman mutlu eder" dedi. McDuff ve Schlenk'in çalışmalarındaki görünümlerinin "orada bir şeyler olduğunun bir göstergesi" olduğunu ekledi.

Onların dönüm noktası niteliğindeki sonuçları, 2012 yılında, alandaki en iyi dergi olarak kabul edilen Annals of Mathematics'te yayınlandı. Sonsuz basamaklı merdiven benzeri yapıların varlığını ortaya çıkardı. Bu "sonsuz merdivenlerdeki" her bir basamağın boyutu, Fibonacci sayılarının bir oranıydı.

Merdiven çıktıkça basamaklar küçüldü ve küçüldü, merdivenin tepesi altın orana çarpıyordu. Ne altın oranın ne de Fibonacci sayılarının, bir topun içine bir şekil sığdırma sorunuyla belirgin bir ilişkisi yoktur. Bu sayıların McDuff ve Schlenk'in çalışmalarında gizlendiğini görmek tuhaftı.

Sonra bu yılın başlarında, McDuff bu gizem için başka bir ipucu ortaya çıkardı. O ve diğerleri, sadece sonsuz sayıda merdiveni değil, karmaşık fraktal yapıları da ortaya çıkardı. Georgia Üniversitesi'nde profesör olan Michael Usher, sonuçlarının "bu tür bir problemde doğal olarak ortaya çıktığını görmeyi uzaktan beklediğim bir şey değil" dedi.

Çalışma, matematiğin görünüşte ilgisiz alanlarındaki gizli kalıpları ortaya çıkardı; bu, önemli bir şeyin yolda olduğuna dair güvenilir bir işarettir.

Hareketin Şekli

Bu problemler, nesnelerin şekillerini koruduğu Öklid geometrisinin tanıdık dünyasında yer almıyor. Bunun yerine, şekillerin fiziksel sistemleri temsil ettiği garip basit geometri kurallarına göre çalışırlar. Örneğin, basit bir sarkaç düşünün. Herhangi bir anda sarkacın fiziksel durumu, nerede olduğu ve ne kadar hızlı gittiği ile tanımlanır. Sarkacın konumu ve hızı gibi bu iki değer için tüm olasılıkları çizerseniz, sonsuz uzunlukta bir silindirin yüzeyine benzeyen basit bir şekil elde edersiniz.

Semplektik şekilleri değiştirebilirsiniz, ancak yalnızca çok özel şekillerde. Nihai sonuç aynı sistemi yansıtmalıdır. Değişebilecek tek şey onu nasıl ölçtüğünüzdür. Bu kurallar, temel fiziği bozmamanızı sağlar.

McDuff ve Schlenk, bir topun içine ne zaman semplektik bir elipsoid -uzun bir damla- sığdırabileceklerini anlamaya çalışıyorlardı. Gömme problemi olarak bilinen bu tür bir problem, şekillerin hiç bükülmediği Öklid geometrisinde oldukça kolaydır. Ayrıca, hacimleri değişmediği sürece şekillerin istediğiniz kadar bükülebildiği diğer geometri alt alanlarında da basittir.

Simplektik geometri daha karmaşıktır. Burada cevap, elipsoidin ne kadar uzamış olduğunu temsil eden bir sayı olan "eksantrikliğine" bağlıdır. Yüksek eksantrikliğe sahip uzun, ince bir şekil, kıvrılan bir yılan gibi kolayca daha kompakt bir şekle katlanabilir. Eksantriklik düşük olduğunda, işler daha az basittir.

McDuff ve Schlenk'in 2012 makalesi, çeşitli elipsoidlere sığabilecek en küçük topun yarıçapını hesapladı. Çözümleri, Fibonacci sayılarına dayanan sonsuz bir merdivene benziyordu - bir sonraki sayının her zaman önceki ikisinin toplamı olduğu bir sayı dizisi.

McDuff ve Schlenk sonuçlarını açıkladıktan sonra, matematikçiler merak içinde kaldılar: Elipsoidinizi toptan başka bir şeye, örneğin dört boyutlu bir kübe yerleştirmeyi denerseniz ne olur? Daha fazla sonsuz merdiven açılır mı?

Fraktal Bir Sürpriz

Araştırmacılar burada birkaç sonsuz merdiven, orada birkaç tane daha ortaya çıkardıkça sonuçlar yavaş yavaş gelmeye başladı. Ardından 2019'da Matematik Kadınları Derneği, semplektik geometri üzerine bir haftalık bir atölye çalışması düzenledi. Etkinlikte, Holm ve işbirlikçisi Ana Rita Pires, McDuff ve California Üniversitesi, Berkeley'den yeni mezun olan Morgan Weiler'ın da dahil olduğu bir çalışma grubu oluşturdu. Elipsoidleri sonsuz sayıda enkarnasyona sahip bir şekle gömmek için yola çıktılar - sonunda sonsuz sayıda merdiven üretmelerine izin verdiler.

Grubun incelediği şekilleri görselleştirmek için, basit şekillerin hareketli nesnelerden oluşan bir sistemi temsil ettiğini unutmayın. Bir nesnenin fiziksel durumu konum ve hız olmak üzere iki nicelik kullandığından, simpletik şekiller her zaman çift sayıda değişkenle tanımlanır. Başka bir deyişle, çift boyutludurlar. İki boyutlu bir şekil, sabit bir yol boyunca hareket eden tek bir nesneyi temsil ettiğinden, dört boyutlu veya daha fazla olan şekiller, matematikçiler için en ilgi çekici olanlardır.

Ancak dört boyutlu şekilleri görselleştirmek imkansız, bu da matematikçilerin araç setini ciddi şekilde sınırlıyor. Kısmi bir çözüm olarak, araştırmacılar bazen şekil hakkında en azından bazı bilgileri yakalayan iki boyutlu resimler çizebilirler. Bu 2B resimleri oluşturma kurallarına göre, dört boyutlu bir top dik üçgen olur.

Holm ve Pires grubunun analiz ettiği şekillere Hirzebruch yüzeyleri denir. Her bir Hirzebruch yüzeyi, bu dik üçgenin üst köşesinden kesilerek elde edilir. Bir sayı, b, ne kadar kestiğinizi ölçer. b 0 olduğunda, hiçbir şeyi kesmemiş olursunuz; 1 olduğunda, neredeyse tüm üçgeni sildiniz.

Başlangıçta, grubun çabaları pek meyve vermeyecek gibi görünüyordu. Şu anda Cornell'de postdoc olan Weiler, "Üzerinde çalışmak için bir hafta harcadık ve hiçbir şey bulamadık" dedi. 2020'nin başlarında, hala fazla ilerleme kaydetmemişlerdi. McDuff, Holm'un yazacakları makalenin başlığına ilişkin önerilerinden birini hatırladı: "Merdiven Bulmakta Şans Yok."

Ancak grup sonunda temellerini buldu ve Ekim 2020'de b'nin belirli değerleri için sonsuz merdiven kazısı yapan bir makale yayınladılar.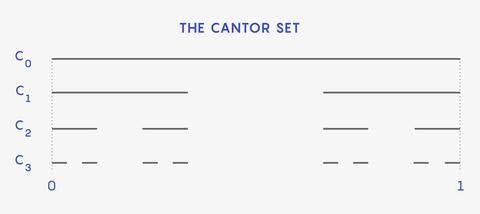

Geçtiğimiz Mart ayında, McDuff, Weiler ve Holm'un bir öğrencisi olan ve koronavirüs pandemisi sırasında McDuff ile çalışmaya başlayan Nicki Magill, Hirzebruch yüzeylerindeki elipsoidlerin yerleşimlerini analiz etme projesini neredeyse tamamladıkları bir ön baskı yayınladılar. "Harika," dedi Holm. "Çok güzel." Bunu yaptıklarında başka bir sürpriz ortaya çıktı. Sonsuz bir merdivenin göründüğü b'nin tüm değerlerine bakarsanız, başka bir fraktal yapı elde edersiniz - sağduyuya meydan okuyan özelliklere sahip noktaların bir düzenlemesi. Cantor kümesi olarak adlandırılır, rasyonel sayılardan daha fazla puana sahiptir - yine de Cantor kümesinin puanları bir şekilde daha dağınıktır. Maryland Üniversitesi'nden bir matematikçi olan Daniel Cristofaro-Gardiner, "Hala tam olarak özümsemeye çalıştığım merdiven simetrileriyle bu güzel resmi gerçekten geliştirdiler" dedi. Yeni çalışma, önceki sonuçlardan daha fazla sonsuz merdiven üretmiş olsa da, Hirzebruch yüzeyleri olası basit şekillerin yalnızca küçük bir kısmını içerdiğinden, simplektik gömmeler ve onlara eşlik eden merdivenler çoğunlukla bir sır olarak kalıyor. Holm, "Hala biraz ormanda olduğumuzu hissediyorum ve resmin tamamını görebileceğimiz bulut seviyesine tam olarak ulaşmadık" dedi. "Heyecan verici bir an, çünkü oraya varacağımızı düşünüyorum."

KAYNAK